2018-Seq2Slate Re-ranking and slate optimization with RNNs

摘要

在排序时，将候选items作为一个有吸引力的整体展示给用户是一个非常重要的任务。直观来看，在将一个item加入到候选集时，需要考虑候选池中已经存在的item的影响。本文提出一个seq2seq排序模型Seq2Slate，在每一个time step，模型考虑到候选集中已经存在的items来决定下一个“best”选择，时序模型能够灵活可扩展地捕捉item之间的关联信息。本文还展示了如何使用弱监督方法端到端训练。

模型

问题建模：条件概率 $p(\pi _{j}|\pi _{<j},x)\in \bigtriangleup ^{n} ，\pi _{<j}=(\pi _{1},…,\pi _{j-1})$,在有j-1个已选择item的情况下，第j个位置选择x的概率 网络结构：Pointer Network

• 标准的seq2seq问题中，输出单词表长度是固定的，只需要预测固定长度单词表的index，但是在推荐场景中排序的items数量可以变化，针对这个问题，Pointer Network使用无参数的softmax指向输入序列中的item。

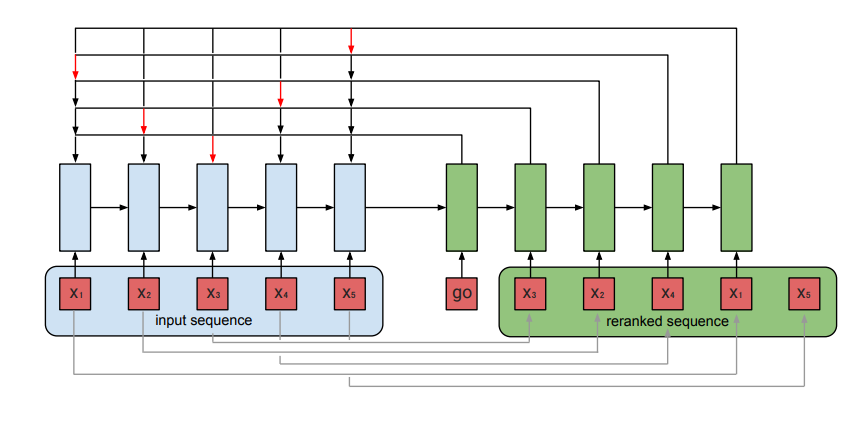
模型包括两个部分，编码器和解码器，两者都使用LSTM单元，

1. 在每一个编码time step $i$，编码器RNN读取第i个item的特征向量$x_{i}$，编码器输出$\rho$维的向量$e_{i}$，输入序列\(\{x_{i}\}_{i=1}^{n}\)被被编码为\(\{e_{i} \} _{i=1}^{n}\)
2. 在decode的每一个步$j$，编码器输出$\rho$维的向量$d_{j}$，作为attention模块的query
3. 在attention，使用query和$e_{i}$计算选择第i个item被放在第j个位置的分数，并使用softmax转化成概率

\[s_{i}^{j} = v^{T}tanh(W_{enc}·e_{i}+W_{dec}·d_{j})\] \[p_{\theta}(\pi_{j}=i|\pi_{<j},x)\equiv p_{i}^{j}=j =\left\{\begin{matrix} e^{s_{i}^{j}}/ {\textstyle \sum_{k\notin \pi<j}e^{s_{k}^{j}}} & \text{if } i\notin \pi_{<j} \\ 0 & \text{if } i\in \pi_{<j} \end{matrix}\right.\]

1. 选择出来的分数最高item作为decoder下一个时刻的输入
2. decoder的初始化输入向量go是一个可学习向量

训练方式

强化学习

暂时跳过

监督学习

基于点击率模型，设二分类label为$y=(y_{1},…,y_{n})$,位置j对每一个item预估的分数集合是$s=(s_{1},…s_{n})$，损失函数$l(s,y)$可以表示为交叉熵损失和hinge loss

\[\ell _{xent}(s,y) = - \sum_{i}\hat{y} _{i}\log{p_{i}}\] \[\ell _{hinge}(s,y) = max({0,1-\min_{i:y_{i}=1}}s_{i}+\max_{j:y_{j}=0}s_{j})\]

其中\(\hat{y_{i}}={y}_{i}/\sum_{j}y_{j}\)，$p_{i}$是softmax的结果，交叉熵损失为了赋予正样本更高的概率，hinge loss最大化正负样本的概率距离，两个函数都是凸函数，为了更好收敛，作者对hinge loss做了变化

最后一个session内整体loss函数，每一步loss计算是会忽略掉已经被指向的item，

\[\mathcal{L}_{\pi}(S,y)=\sum_{j=1}^{n} w_{j}\ell_{\pi<j}(s_{j},y)\]

$w_{j}= 1/log(j+1)$，是一个随time step衰减的值

Bello I, Kulkarni S, Jain S, et al. Seq2Slate: Re-ranking and slate optimization with RNNs[J]. arXiv preprint arXiv:1810.02019, 2018.