2017-Deep Interest Network for Click-Through Rate Prediction
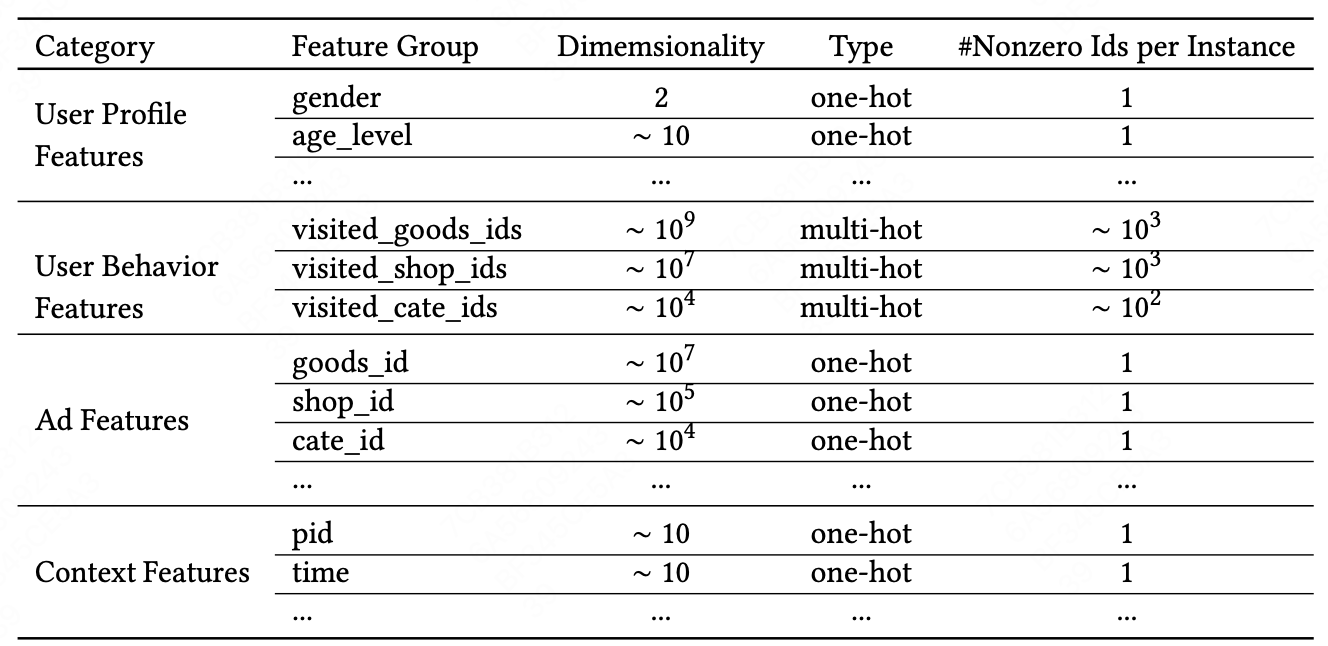
特征表示
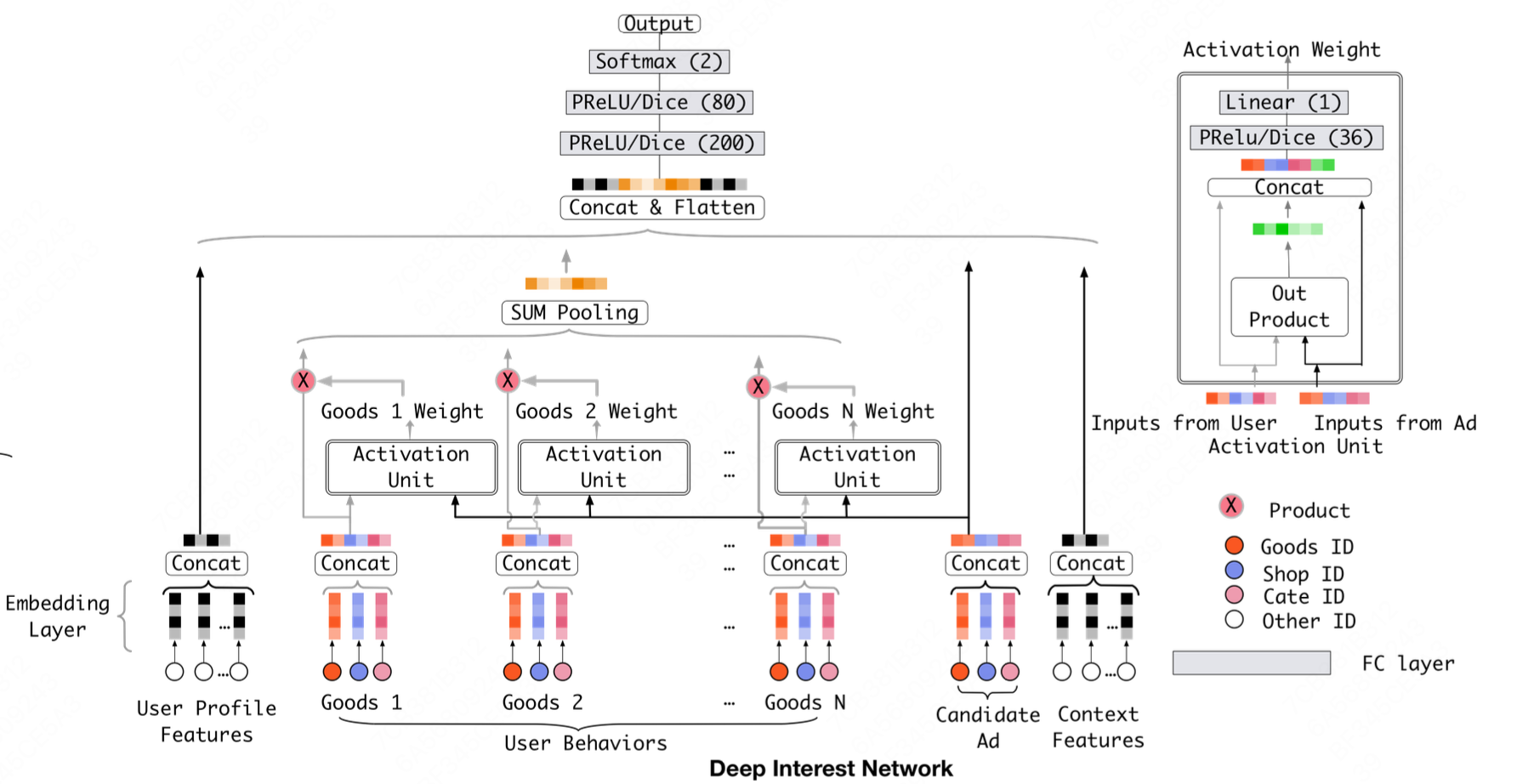
base model
四个主要模块
- Embedding Layer
- 输入特征为稀疏二值编码,embedding层将sparse特征编码为dense特征
- Pooling layer and Concat layer
- 将用户历史行为序列特征通过sum pooling转化为固定长度的向量
- MLP
- Loss
为什么要提出DIN模型? 用户在浏览电商网站时表现出来的兴趣具有多样性,只有部分的用户历史数据会影响到当次的推荐物品是否会点击,时间更接近的行为相比时间更远的行为对本次是否点击的影响也不同。因此,在模型预测的时候,需要对不同的历史行为赋予不同的权重。
DIN model
DIN模型在用户历史行为embedding模块新增了Activation Unit,使用用户历史行为item embedding和候选item embedding作为输入,通过一个前馈神经网络输出注意力权重。 在给定候选广告A的情况下,用户历史行为序列表征计算方式为:
\[v_{U}(A)=f(v_{A},e_1,e_2...e_H) =\sum_{j=1}^{H}a(e_{j},v_{A})e_{j}=\sum_{j=1}^{H}w_{j}e_{j}\]\(\{e_1,e_2...e_H\}\)记为用户$U$的历史行为序列的embedding,\(v_A\)是候选广告表征向量。用户历史行为表征向量变成了加权求和。每一个不同的candidate都对应不同的用户历史行为表征。最后通过Sum Pooling将特征聚合在一起。
训练技巧
Dice激活函数
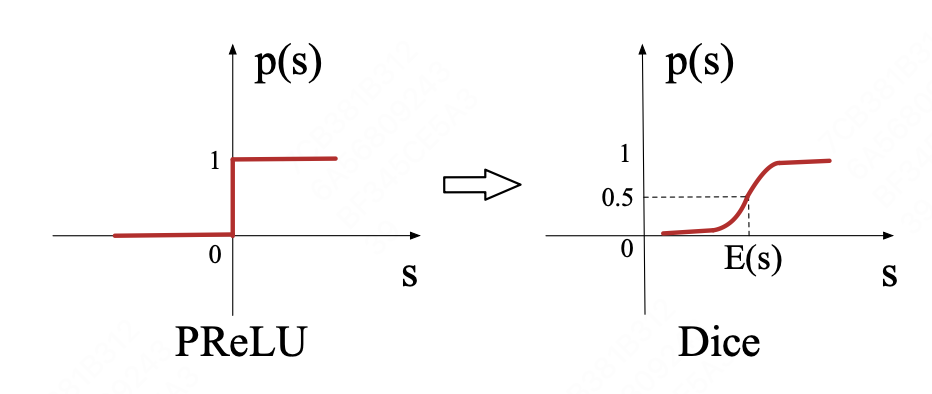
对PRelu的一种扩展。在PRelu中,
\[f(s)=\begin{cases}s & \text{ if } s>0 \\ \alpha s & \text{ if } s<=0 \end{cases}=p(s)·s+(1-p(s))·\alpha s\]本文中将$p(s)$看作一个控制函数,PRelu的$p(s)$函数如上图所示,将转折点严格限制在0处。实际上,在不同的数据分布中,这个参数是可以调整的。本文提出$\pmb{Dice}$激活函数,他的$p(s)$控制函数为
\[p(s) = \frac{1}{1+e^{-\frac{s-E[s]}{\sqrt{Var[s]+\varepsilon } } }}\]$E(s)$和$Var(s)$是每一个mini-batch中数据的均值和方差
自适应正则化
背景:在没有任何正则化的情况下,模型训练在一个epoch后下降,L1和L2等方法,当有上亿参数时计算每个mini-batch下所有参数的L2正则化,计算量太大。
解决方案:由于特征的稀疏编码特性,大多数的参数集中于embedding dictionary,每一个mini-batch的训练只对稀疏向量对应位置非0的embedding进行更新,只对这些参数进行正则化会大大减少计算量。