推荐系统中的的多任务模型(MMoE、ESMM、PLE)
ESMM
阿里妈妈团队SIGIR’2018,在广告推荐场景中,基于多任务学习的思路,提出一种新的CVR预估模型。
Motivation
CVR预估有两个问题:
- 转化是在点击之后才有可能发生的动作,实际正负样本应该是点击且转化和点击未转化,但是模型实际训练过程中,使用的是整个空间的样本。
- CVR训练样本中的点击样本数量远小于CTR的训练使用的曝光样本。
Model
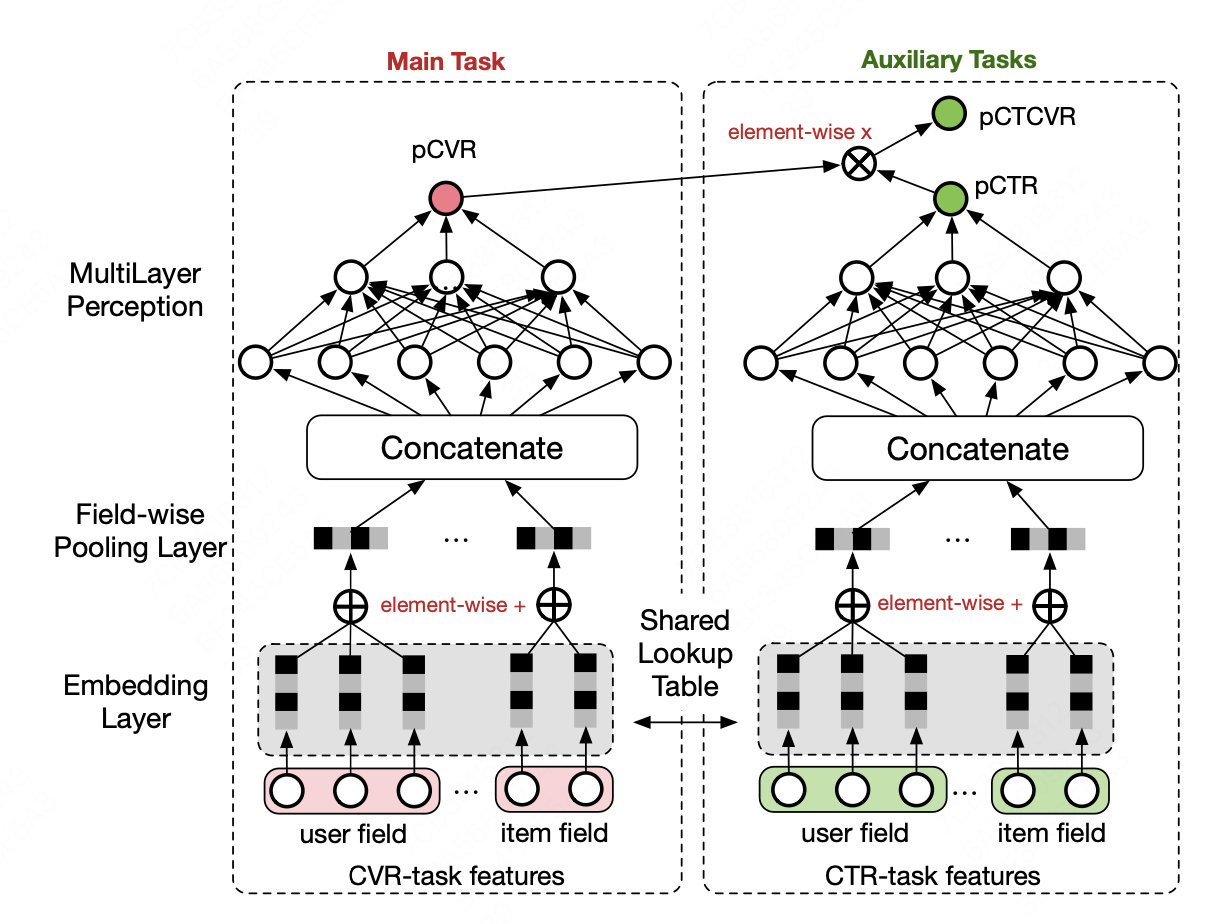
点击(CTR)、转化(CVR)、点击然后转化(CTCVR)三个任务中,CTR与CVR没有直接的相关关系。 模型分为两个模块,左侧预测$p_{CVR}$,右侧预测$p_{CTR}$,并使用$p_{CVR}$和$p_{CTR}$的乘积计算$p_{CTCVR}$
表现在损失函数上
\[L(\theta_{cvr},\theta_{ctr})=\sum_{i=1}^{N}l(y_{i},f(x_{i};\theta_{ctr}))+\sum_{i=1}^{N}l(y_{i}\And z_{i},f(x_{i};\theta_{ctr})*f(x_{i};\theta_{cvr})\]利用CTCVR和CTR作为监督训练,隐式学习CVR的信息
MMoE
Motivation
在大规模推荐系统中,模型往往需要学习多个目标,传统的share-bottom结构可能受到任务差异和数据差异带来的影响,子任务差距过大会导致模型训练效果不佳。为了考虑多任务之间的差异性,google团队提出MMoE结构。(KDD 2018)
Shared-bottom Multi-task Model
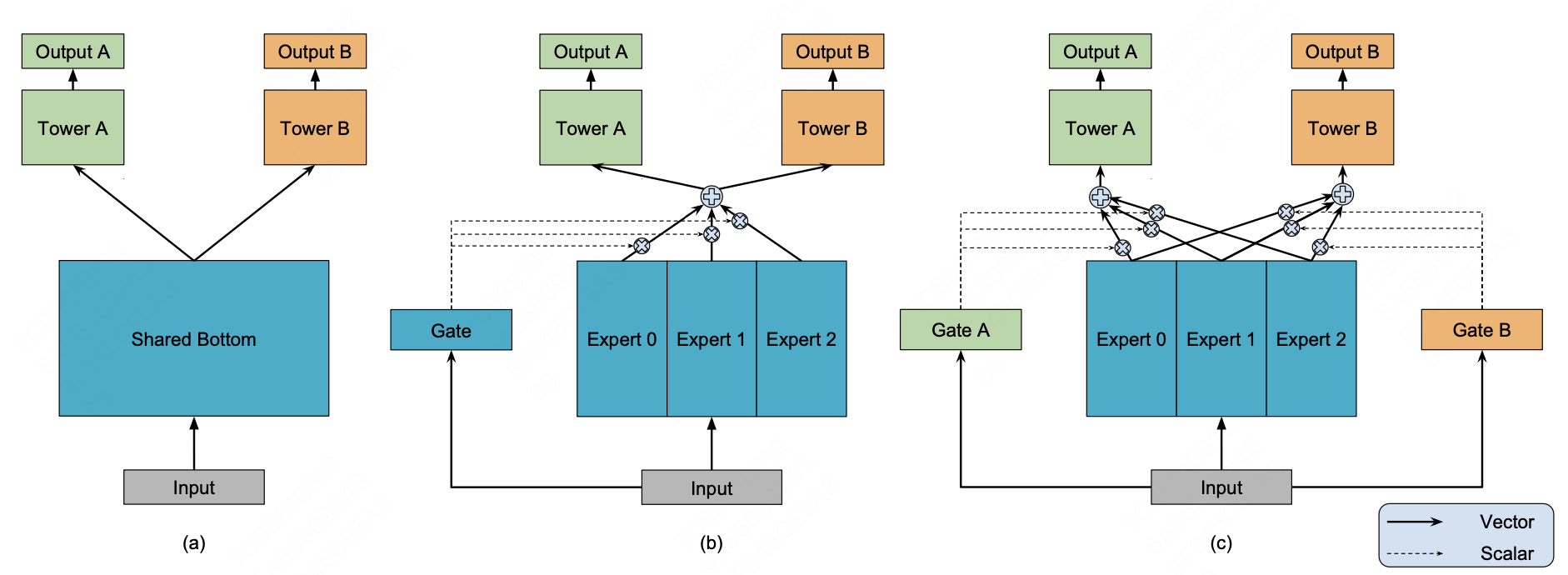
图(a)中所示是常用的shared-bottom多任务学习模型,多个任务共享底层神经网络,表示为函数$f$,使用$k$个tower network分别预测每一个子任务。\(y_{k} = h^{k}(f(x))\)
Mixture-of-Experts(MoE)
MoE是将shared-bottom部分拆分为n个expert网络$f_{i},i=1,2…n$,共享输入。通过gating network产生n个experts上的概率分布。最终输出是所有expert的加权求和。 \(y = \sum_{i=1}^{n}g(x)_{i}f_{i}(x)\),其中,\(\sum_{i=1}^{n}g(x)_{i}=1\)
MMoE模型
MMoE模型中,对每一个task k计算单独单独计算矩阵expert上的权重
\[y_{k} =h^{k}f(x)_{k},f(x)_{k} = \sum_{i=1}^{n}g^{k}(x)_{i}f_{i}(x)\]其中\(g_{k}(x) = softmax(W_{gk}x)\)
PLE
腾讯RecSys’20 Best Paper
Motivation
多任务学习并被证明可以通过任务之间的信息共享来提高学习效率。 然而,多个任务经常是松散相关甚至是相互冲突的,这可能导致性能恶化,发现现有的 MTL 模型经常以牺牲其他任务的性能为代价来改进某些任务,当任务相关性很复杂并且有时依赖于样本时,即与相应的单任务模型相比,多个任务无法同时改进,论文中称之为跷跷板现象。
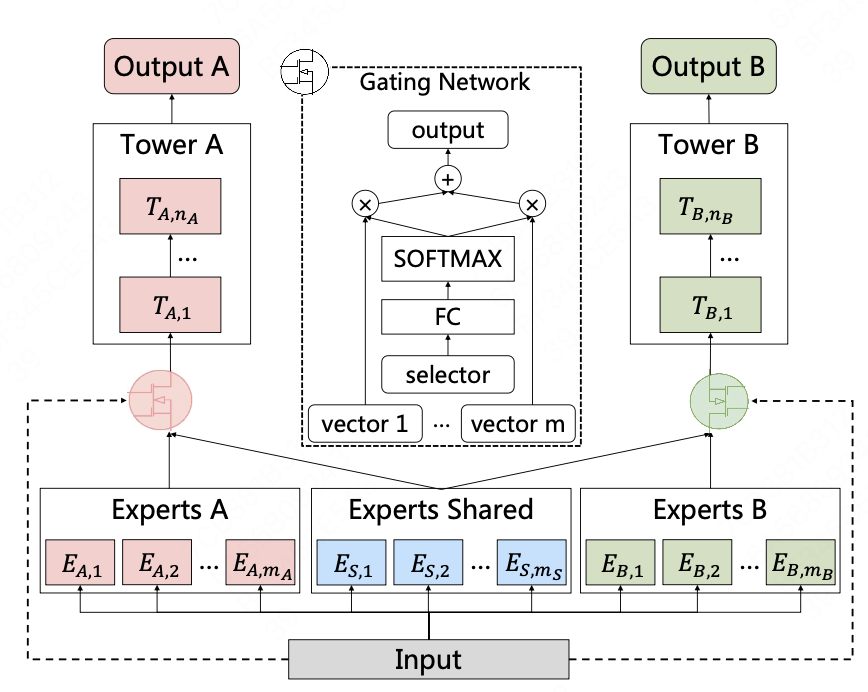
CGC
论文在MMoE的基础上分离出shared-expert和task-specific-expert
任务k的门控网络\(g^{k}(x)=w^{k}(x)S^{k}(x)\),$x$是模型输入向量,\(w^{k}(x)\)通过输入向量线性变换,再经过softmax层生成选择概率。 \(S^{k}(x)\)是任务k的expert和共享expert的拼接向量
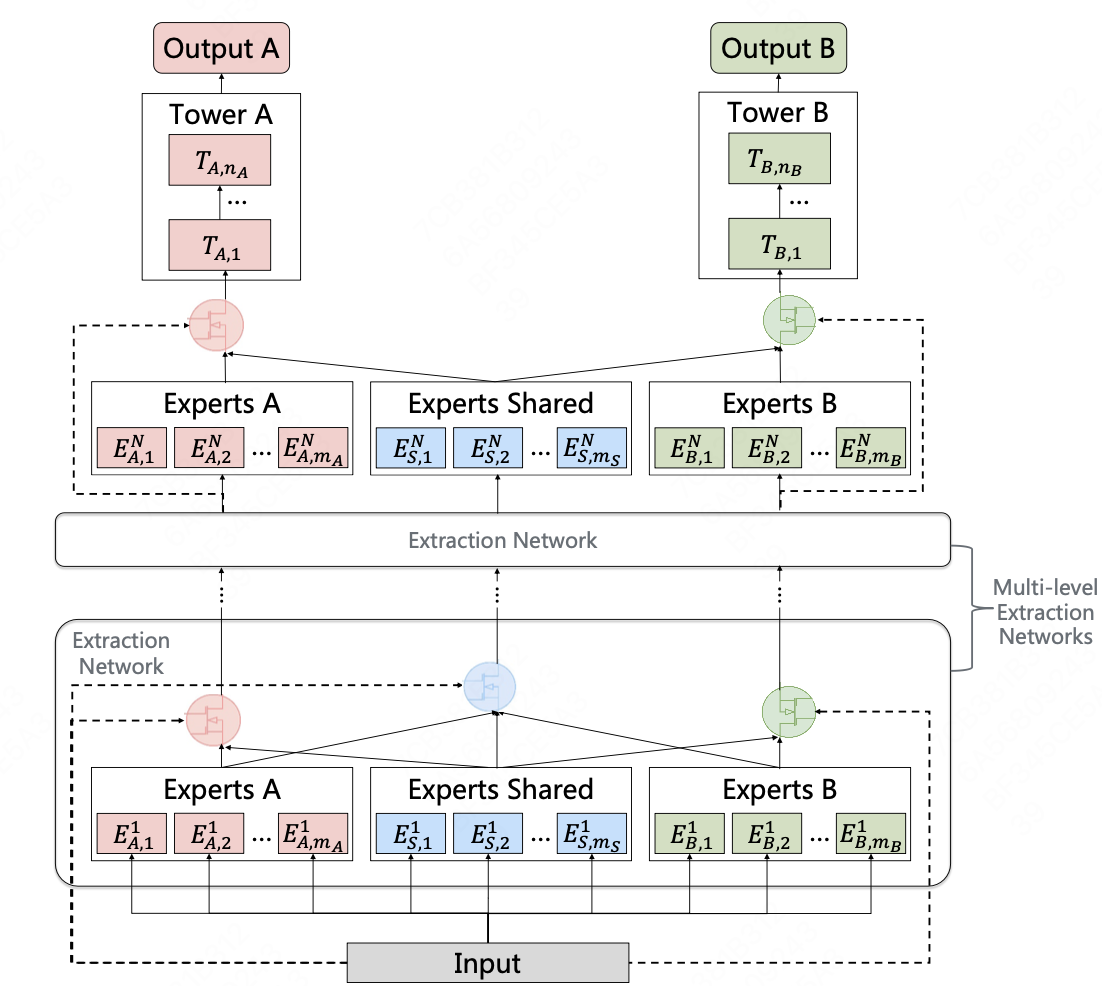
PLE
PLE将单层CGC结构扩展到了多层